ナンプレを解くプログラムを書いてみる【1】バックトラック法
ちょっとナンプレ(数独)を解いてみようと思った。ふと。
というのは半分冗談で、仕組みが分かっているものをプログラムで機械的に動作させる、良い練習サンプルとして優秀だと思ったからだ。
当然この手のプログラムは昔から開発されているので目新しくはないが、自分でやってみることを最大の目標とする。
例のごとくlaravelをしている。コードは効率よりも理解しやすさを優先して記述している点は、ご了承くだされ。
【前提】ナンプレのルール
決まったルールに沿って、9×9のマス目を1から9の数字で埋める知的な遊び。そのルールとは、横1行、縦1列、3×3に分割された1ブロックには、それぞれ1から9のすべての数字が1回ずつ使われるというルール。シンプルなルールだけど、初期に配置されている数字によって難易度は激変する。
通常は、紙とペンを用意して、あーでもないこーでもないと自力で解く遊びですが、これをプログラムに解かせてみる。
アルゴリズム
今回はバックトラック法を使って解いてみる。空欄マスを対象に、仮の数字を順に当てはめてい仮の条件を満たすパターンがない場合は、一つ戻って次の数字を再度試す。条件を満たしながら、最後まで数字を埋めることが出来れば、それが答えとなる。
人間には不可能なプログラムならではの解法です。最適な組み合わせを探すような問題では、このようなアルゴリズムを使う事が多い。逆に言うと、それ以外の解法を思いつかなくても、全部試して強引に導きだそうとする手法とも言える。
基本の変数の構造
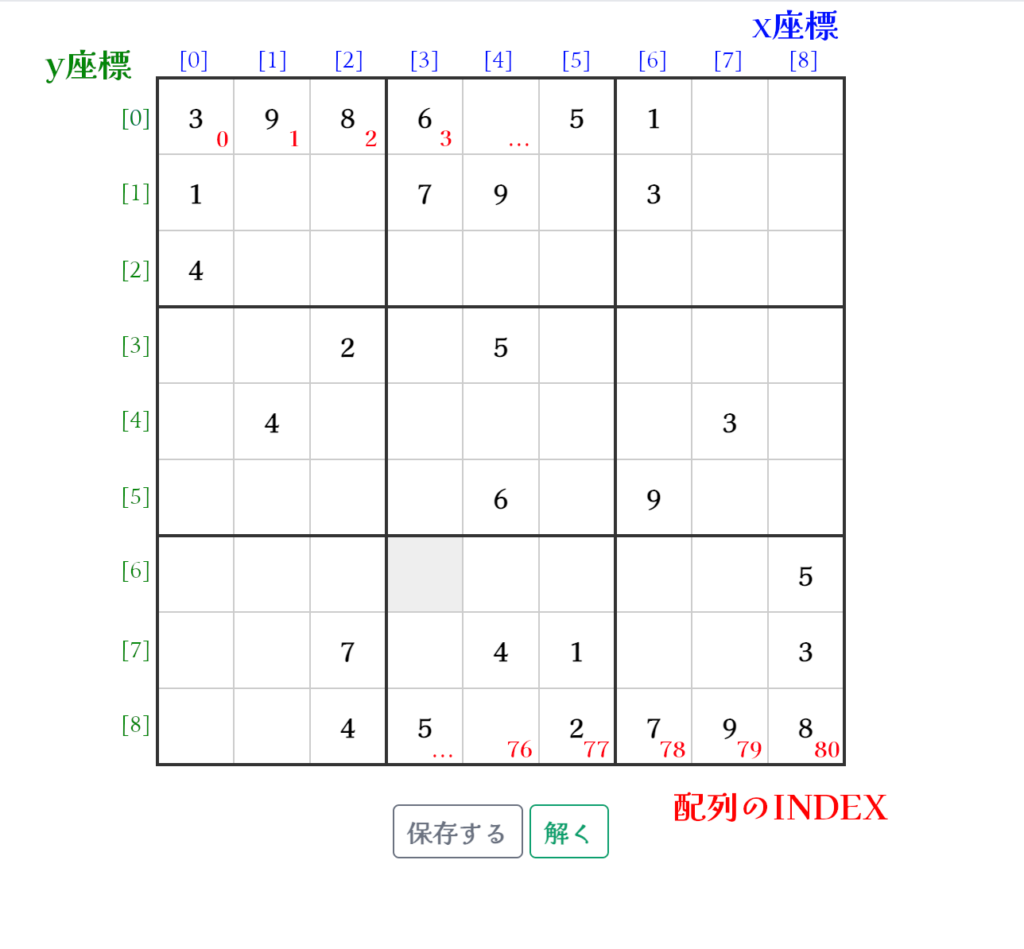
フィールド全体の数値を、INDEXが0から始まる合計81要素の配列として管理します。空の状態は「0」を入れて管理します。図にように、左上から順にx座標とy座標をおくと、INDEXは
インデックス = ( y座標 * 9 ) + x座標
※ 9は1行におけるマス目の数です。で表せます。これは表を使ってロジックを組んだことがあればすんなりだとは思いますが、ピンと来ない人は、眺めてみてください。
処理の流れ
- 次の空白マスを探す
- そのマスに、条件を満たす数字を1個仮に入れる
- 次の空白マスを探す
- そのマスに、条件を満たす数字を1個仮に入れる
を繰り返し、あるマスで条件を満たす数字がなくなった場合、それまでの条件が間違っていたことになるので、
- ひとつ前に戻り、条件を満たす別の数字を1個仮に入れる
- 次の空白マスを探す
という作業を繰り返します。プログラムで言えば、「再帰」を使うことになります。
最後のマスまで値が埋まれば、すべての数値が条件を満たしていることになり、完成となります。
具体的な処理内容の前に
自分で実装してみたい方がいるかもしれないので、実装前の状態も残しておきました。(ブランチ)
https://github.com/supilog/numsolve/tree/BRANCH_INIT
「BRANCH_INIT」から開発にチャレンジしてみることが可能です。おまけとして、以下がついています。
- サンプル問題入りのseeder(QuestionsTableSeeder)
- 問題を新規登録できるWEB画面&処理(Controller&View&Lib)
- 単に解答プログラムをコマンド実行するコマンドクラスの枠組み(NsCommand)
処理内容
これから説明する内容は、以下のクラスの中身についてです。実物はこちら。ブランチは「BRANCH_BACKTRACK」です。
https://github.com/supilog/numsolve/blob/BRANCH_BACKTRACK/app/Libs/NsSolveLib.php
※ laravelの基本処理の説明はここでは行いませんが、不明な場合はブランチ内を覗いてみてください。
メイン処理
public function nmplBackTrack($field, $point): void
{
// 空フィールドを探す
$point = $this->getEmptyPoint($field, $point);
// 空フィールドがない場合
if (empty($point)) {
// 終了前全チェック
if (!$this->isComplete($field)) {
// チェック失敗時にとくにやることがないのでとりあえずExceptionを投げておくことにする。
throw new NumSolveException('エラー発生。おそらくバグですよ');
}
// 返却
$this->comple_field = $field;
return;
}
// 空フィールドがある場合は1から順に数字を入れてチェック
for ($i = 0; $i < 9; $i++) {
$num = $i + 1;
if ($this->isPossibleValue($field, $point, $num)) {
// 入力可能な場合は値をセットして、次のフィールドの探索
$index = $this->coordinatesToIndex($point);
$field[$index] = $num;
$this->nmplBackTrack($field, $point);
}
}
}引数の$fieldは、問題の初期状態を81要素の配列にしたもの(空白は0と表す。)、引数の$pointは、[‘x’=>0, ‘y’=>0]の配列が、それぞれ初期値として入ってきます。
「空フィールドを探す」→「空フィールドがある場合は1から順に数字を入れる」→「次の空フィールドを探す」という再帰で記述されています。
何回も出てくるので、座標からindexを取得するメソッドを作っておいた
/**
* 座標を配列indexに置き換える
* array('x' => x座標, 'y' => y座標) to index
*/
public function coordinatesToIndex($point): int
{
return config('ns.nmpl.size.x') * $point['y'] + $point['x'];
}
これは変数の定義のところでお話した内容です。行のマス目数は設定ファイルに記述したので、config(‘ns.nmpl.size.x’)で呼び出しています。9が設定されています。
空フィールドを探す
/**
* 次の空フィールドを取得
* (現在位置も含む)
* array $point 現在位置の座標
* array $field 全体の値
*/
public function getEmptyPoint($field, $point): array
{
$size_x = config('ns.nmpl.size.x'); // 9
$size_y = config('ns.nmpl.size.y'); // 9
// 空フィールド判定
while ($point['y'] < $size_y) {
while ($point['x'] < $size_x) {
if ($field[$this->coordinatesToIndex($point)] == 0) {
return $point;
}
$point['x']++;
}
$point['y']++;
$point['x'] = 0;
}
// 空フィールドが存在しない場合、空配列を返却する
return array();
}与えられた現在値($point)をもとに、次の空白を探しています。
特定のマスに値を入力できるかチェック
/**
* 入力可能な値かチェック
*/
public function isPossibleValue($field, $point, $num): bool
{
// 0がセットされた要素数10の配列(値がない欄に0が入っているため)
$checklist = array_fill(0, 10, 0);
// 関連indexの取得
$indexes = $this->getRelatedFieldIndex($point);
foreach ($indexes as $index) {
$checklist[$field[$index]] = 1;
}
// チェックリストに1が入っていた場合、その値は存在するので不可
if ($checklist[$num] == 1) {
return false;
}
return true;
}
/**
* 座標から自身を除いた関連マスのindexリストを取得(横、縦、ブロック)
*/
public function getRelatedFieldIndex($point): array
{
$size_x = config('ns.nmpl.size.x'); // 9
$size_y = config('ns.nmpl.size.y'); // 9
$check = array();
// 横
for ($i = 0; $i < $size_x; $i++) {
$index = $this->coordinatesToIndex(['x' => $i, 'y' => $point['y']]);
$check[$index] = 1;
}
// 縦
for ($i = 0; $i < $size_y; $i++) {
$index = $this->coordinatesToIndex(['x' => $point['x'], 'y' => $i]);
$check[$index] = 1;
}
// ブロック
$block_init['x'] = floor($point['x'] / 3) * 3;
$block_init['y'] = floor($point['y'] / 3) * 3;
for ($j = 0; $j < 3; $j++) {
for ($i = 0; $i < 3; $i++) {
$x = $block_init['x'] + $i;
$y = $block_init['y'] + $j;
$index = $this->coordinatesToIndex(['x' => $x, 'y' => $y]);
$check[$index] = 1;
}
}
// 自身のindexを除外
$excludeIndex = $this->coordinatesToIndex($point);
unset($check[$excludeIndex]);
return array_keys($check);
}
関連マスの配列indexを調べて、その要素に何の数字が入っているのかをチェックしています。関連するマスにまだ含まれていない数字だったら入力可能という意味でtrueを返却しています。
例えば、「このマスに1を入力しても大丈夫かい?」というメソッドですので、そのマスに関連する縦のマス、横のマス、ブロックのマスの値を調べて、1が存在しなければtrueということです。
終了処理として全チェック
全てのマスが埋まった時点で、解き終わったということなので不要なのですが、今後すべての値をチェックするような処理が欲しくなるかもしれないので、あえて作っただけです。この処理を通さなくても、実行完了といえます。
/**
* 完成チェック
*/
public function isComplete($field): bool
{
$size_x = config('ns.nmpl.size.x'); // 9
$size_y = config('ns.nmpl.size.y'); // 9
// 空フィールド確認
if (in_array(0, $field)) {
return false;
}
// 関連マスに自身の値が存在しないことを全てのマスで確認
$result = true;
for ($j = 0; $j < $size_y; $j++) {
for ($i = 0; $i < $size_x; $i++) {
// 自身の座標
$point = ['x' => $i, 'y' => $j];
// 自身のINDEX
$current_index = $this->coordinatesToIndex($point);
// 自身の値
$current_value = $field[$current_index];
// 関連INDEX
$relatedIndexes = $this->getRelatedFieldIndex($point);
// 関連INDEXのマスに自身の値が入っていないかチェック
foreach ($relatedIndexes as $relatedIndex) {
if ($current_value == $field[$relatedIndex]) {
$result = false;
}
}
}
}
return $result;
}実行
$ php artisan ns:solve 1
Q:
------------------
3,9,8,6,0,5,1,0,0,
1,0,0,7,9,0,3,0,0,
4,0,0,0,0,0,0,0,0,
0,0,2,0,5,0,0,0,0,
0,4,0,0,0,0,0,3,0,
0,0,0,0,6,0,9,0,0,
0,0,0,0,0,0,0,0,5,
0,0,7,0,4,1,0,0,3,
0,0,4,5,0,2,7,9,8,
------------------
A:
------------------
3,9,8,6,2,5,1,7,4,
1,2,5,7,9,4,3,8,6,
4,7,6,1,8,3,5,2,9,
7,6,2,3,5,9,8,4,1,
5,4,9,2,1,8,6,3,7,
8,3,1,4,6,7,9,5,2,
2,8,3,9,7,6,4,1,5,
9,5,7,8,4,1,2,6,3,
6,1,4,5,3,2,7,9,8,
------------------
実行時間 : 20sec時間はかかっていますが、処理できているようです。無事成功!
まとめ
今回は再帰的に解答を求めて見ました。最適化などは一切行っていないので、速度に関してはノーコメントで!
改善ポイントは沢山あるでしょうが、一例としては、
- 1から9まで順に入力できるかチェックしているが、可能な値しか試さない
- indexの若い順に再帰をしているが、入力可能な要素数の小さい順に再帰をする
- 人間的な解法で確定できるマスを先に埋める
など。
再帰的なプログラムでの解法は、わりと簡単に書けて、しかも強力なんですよね。「全部試すんだから、いつかは辿り着けるじゃん」の精神。
人間的な解法をプログラムに落とし込むのも、ちょっと次にやってみたいと思います。それでは!
















